About




multivar_horner is a python package implementing a multivariate Horner scheme (“Horner’s method”, “Horner’s rule”)[1] for efficiently evaluating multivariate polynomials.
For an explanation of multivariate Horner factorisations and the terminology used here refer to e.g. Greedy algorithms for optimizing multivariate Horner schemes [2]
A given input polynomial in canonical form (or normal form) is being factorised according to the greedy heuristic described in [2] with some additional computational tweaks.
The resulting Horner factorisation requires less operations for evaluation and is being computed by growing a “Horner Factorisation Tree”.
When the polynomial is fully factorized (= all leaves cannot be factorised any more), a computational “recipe” for evaluating the polynomial is being compiled.
This “recipe” (stored internally as numpy arrays) enables computationally efficient evaluation.
Numba just in time compiled functions operating on the numpy arrays make this fast.
All factors appearing in the factorisation are being evaluated only once (reusing computed values).
Pros:
Cons:
increased initial computational requirements and memory to find and then store the factorisation
The impact of computing Horner factorisations has been evaluated in the benchmarks below.
With this package it is also possible to represent polynomials in canonical form and to search for an optimal Horner factorisation.
Also see: GitHub, PyPI, arXiv paper
Dependencies
python>=3.6,
numpy>=1.16,
numba>=0.48
License
multivar_horner is distributed under the terms of the MIT license
(see LICENSE).
Benchmarks
To obtain meaningful results the benchmarks presented here use polynomials sampled randomly with the following procedure: In order to draw polynomials with uniformly random occupancy, the probability of monomials being present is picked randomly. For a fixed maximal degree n in m dimensions there are (n+1)^m possible exponent vectors corresponding to monomials. Each of these monomials is being activated with the chosen probability.
Refer to [5] for an exact definition of the maximal degree.
For each maximal degree up to 7 and until dimensionality 7, 5 polynomials were drawn randomly. Note that even though the original monomials are not actually present in a Horner factorisation, the amount of coefficients however is identical to the amount of coefficients of its canonical form.
Even though the amount of operations required for evaluating the polynomials grow exponentially with their size irrespective of the representation, the rate of growth is lower for the Horner factorisation.
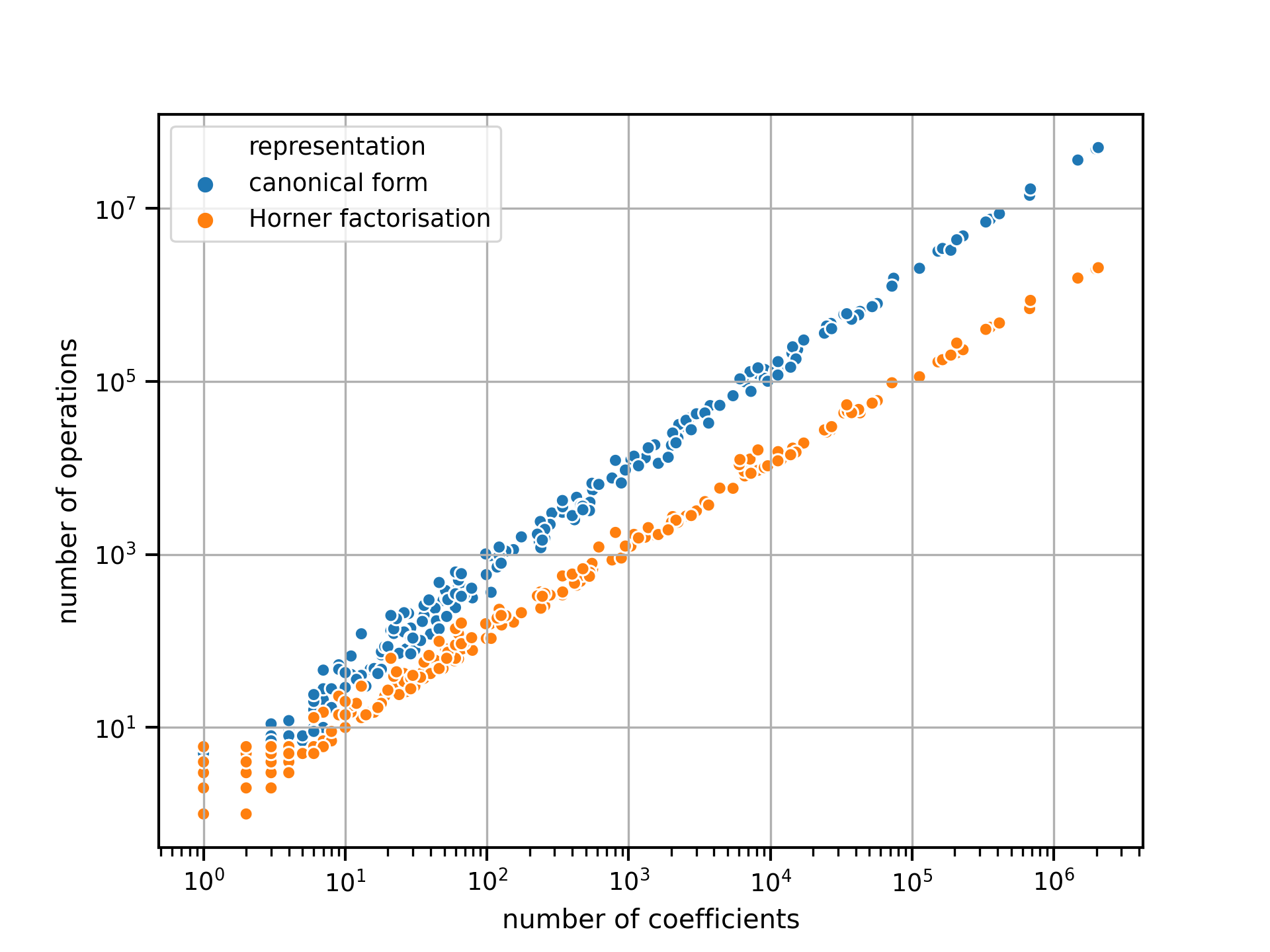
amount of operations required to evaluate randomly generated polynomials.
Due to this, the bigger the polynomial the more compact the Horner factorisation representation is relative to the canonical form. As a result the Horner factorisations are computationally easier to evaluate.
Numerical error
In order to compute the numerical error, each polynomial has been evaluated at a point chosen uniformly random from $[-1; 1]^m$ with the different methods. The polynomial evaluation algorithms use 64-bit floating point numbers, whereas the ground truth has been computed with 128-bit accuracy in order to avoid numerical errors in the ground truth value. To receive more representative results, the obtained numerical error is being averaged over 100 tries with uniformly random coefficients each in the range $[-1; 1]$, All errors are displayed as (averaged) absolute values.
With increasing size in terms of the amount of included coefficients the numerical error of both the canonical form and the Horner factorisation found by multivar_horner grow exponentially.
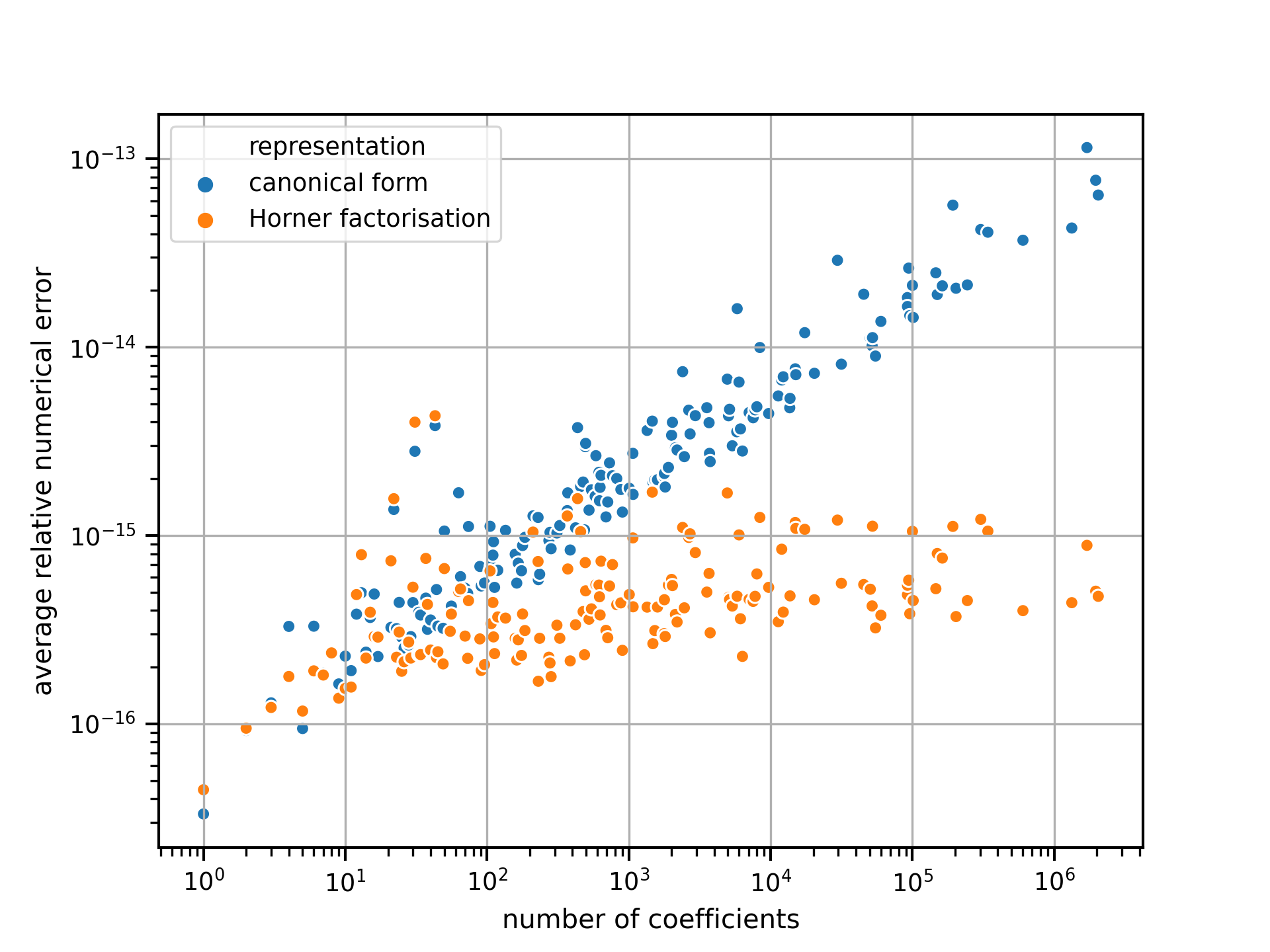
numerical error of evaluating randomly generated polynomials of varying sizes.
In comparison to the canonical form however the Horner factorisation is much more numerically stable. This has also been visualised in the following figure:
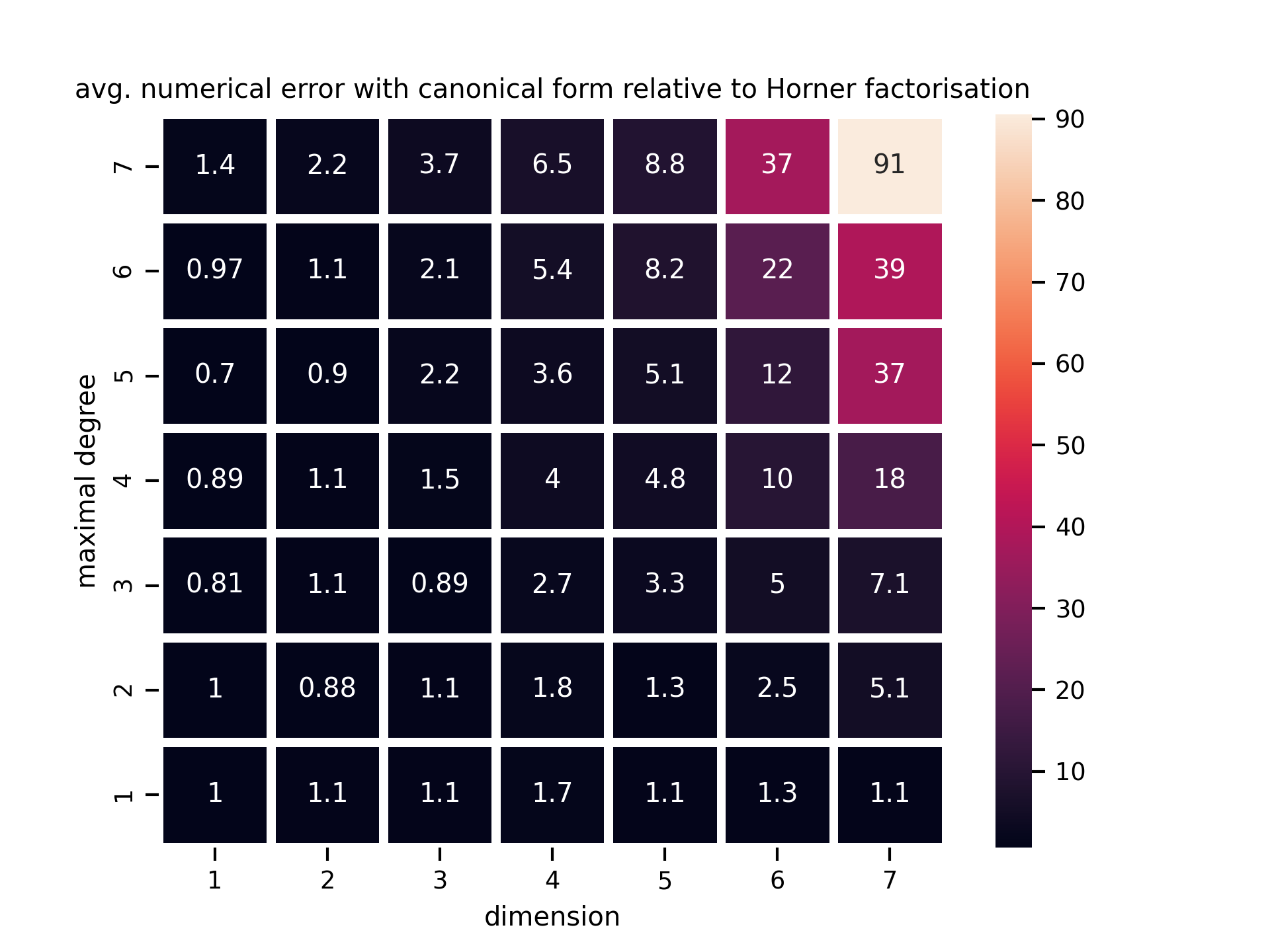
numerical error of evaluating randomly generated polynomials in canonical form relative to the Horner factorisation.
Note
if you require an even higher numerical stability you can set FLOAT_DTYPE = numpy.float128
or FLOAT_DTYPE = numpy.longfloat in global_settings.py.
Then however the jit compilation has to be removed in helper_fcts_numba.py (Numba does not support float128).
Speed tests
The following speed benchmarks have been performed on a 2017 MacBook Pro: 4x2,8 GHz Intel Core i7 CPU, 16 GB 2133 MHz LPDDR3 RAM, macOS 10.13 High Sierra.
The software versions in use were: multivar_horner 2.0.0, python 3.8.2, numpy 1.18.1 and numba 0.48.0
Both evaluation algorithms (with and without Horner factorisation) make use of Numba just in time compiled functions.
Speed test:
testing 100 evenly distributed random polynomials
average timings per polynomial:
parameters | setup time (s) | eval time (s) | # operations | lucrative after
dim | max_deg | canonical | horner | delta | canonical | horner | delta | canonical | horner | delta | # evals
================================================================================================================================================================
1 | 1 | 4.90e-05 | 2.33e-04 | 3.8 x more | 8.96e-06 | 1.28e-05 | 0.4 x more | 3 | 1 | 2.0 x less | -
1 | 2 | 5.24e-05 | 1.95e-04 | 2.7 x more | 3.42e-06 | 6.01e-06 | 0.8 x more | 4 | 2 | 1.0 x less | -
1 | 3 | 5.07e-05 | 2.31e-04 | 3.6 x more | 3.48e-06 | 5.86e-06 | 0.7 x more | 6 | 3 | 1.0 x less | -
1 | 4 | 5.04e-05 | 2.65e-04 | 4.3 x more | 3.59e-06 | 5.62e-06 | 0.6 x more | 7 | 4 | 0.8 x less | -
1 | 5 | 5.08e-05 | 3.04e-04 | 5.0 x more | 3.49e-06 | 8.47e-06 | 1.4 x more | 8 | 6 | 0.3 x less | -
1 | 6 | 4.81e-05 | 4.65e-04 | 8.7 x more | 3.54e-06 | 6.72e-06 | 0.9 x more | 10 | 7 | 0.4 x less | -
1 | 7 | 5.39e-05 | 4.00e-04 | 6.4 x more | 3.95e-06 | 6.49e-06 | 0.6 x more | 12 | 8 | 0.5 x less | -
1 | 8 | 5.19e-05 | 3.83e-04 | 6.4 x more | 5.63e-06 | 6.16e-06 | 0.1 x more | 12 | 8 | 0.5 x less | -
1 | 9 | 4.88e-05 | 4.42e-04 | 8.0 x more | 3.73e-06 | 6.05e-06 | 0.6 x more | 14 | 10 | 0.4 x less | -
1 | 10 | 4.89e-05 | 5.41e-04 | 10 x more | 3.80e-06 | 7.11e-06 | 0.9 x more | 15 | 10 | 0.5 x less | -
2 | 1 | 8.34e-05 | 3.11e-04 | 2.7 x more | 3.85e-06 | 6.09e-06 | 0.6 x more | 11 | 3 | 2.7 x less | -
2 | 2 | 4.96e-05 | 7.05e-04 | 13 x more | 3.80e-06 | 5.82e-06 | 0.5 x more | 26 | 10 | 1.6 x less | -
2 | 3 | 5.20e-05 | 9.75e-04 | 18 x more | 4.50e-06 | 6.70e-06 | 0.5 x more | 38 | 16 | 1.4 x less | -
2 | 4 | 5.93e-05 | 1.44e-03 | 23 x more | 5.53e-06 | 7.12e-06 | 0.3 x more | 63 | 27 | 1.3 x less | -
2 | 5 | 5.26e-05 | 2.25e-03 | 42 x more | 6.49e-06 | 6.46e-06 | -0.0 x more | 91 | 39 | 1.3 x less | 59828
2 | 6 | 5.31e-05 | 2.90e-03 | 54 x more | 7.65e-06 | 6.55e-06 | 0.2 x less | 127 | 54 | 1.4 x less | 2595
2 | 7 | 5.72e-05 | 3.76e-03 | 65 x more | 9.02e-06 | 6.03e-06 | 0.5 x less | 164 | 70 | 1.3 x less | 1238
2 | 8 | 5.32e-05 | 4.39e-03 | 81 x more | 9.71e-06 | 6.06e-06 | 0.6 x less | 198 | 84 | 1.4 x less | 1186
2 | 9 | 5.27e-05 | 5.04e-03 | 95 x more | 1.08e-05 | 7.25e-06 | 0.5 x less | 230 | 99 | 1.3 x less | 1418
2 | 10 | 5.47e-05 | 6.74e-03 | 122 x more | 1.36e-05 | 6.46e-06 | 1.1 x less | 310 | 132 | 1.3 x less | 935
3 | 1 | 4.96e-05 | 5.69e-04 | 10 x more | 3.70e-06 | 6.18e-06 | 0.7 x more | 26 | 7 | 2.7 x less | -
3 | 2 | 5.34e-05 | 2.02e-03 | 37 x more | 5.43e-06 | 6.70e-06 | 0.2 x more | 97 | 28 | 2.5 x less | -
3 | 3 | 5.42e-05 | 4.47e-03 | 82 x more | 8.88e-06 | 6.13e-06 | 0.4 x less | 222 | 68 | 2.3 x less | 1605
3 | 4 | 5.59e-05 | 8.40e-03 | 149 x more | 1.44e-05 | 6.92e-06 | 1.1 x less | 434 | 133 | 2.3 x less | 1115
3 | 5 | 5.73e-05 | 1.35e-02 | 236 x more | 2.10e-05 | 1.36e-05 | 0.5 x less | 685 | 211 | 2.2 x less | 1809
3 | 6 | 7.70e-05 | 2.32e-02 | 300 x more | 3.72e-05 | 8.75e-06 | 3.3 x less | 1159 | 355 | 2.3 x less | 811
3 | 7 | 6.86e-05 | 3.46e-02 | 504 x more | 5.71e-05 | 8.90e-06 | 5.4 x less | 1787 | 543 | 2.3 x less | 717
3 | 8 | 7.07e-05 | 4.64e-02 | 655 x more | 6.97e-05 | 9.97e-06 | 6.0 x less | 2402 | 730 | 2.3 x less | 775
3 | 9 | 8.34e-05 | 6.90e-02 | 826 x more | 1.05e-04 | 1.15e-05 | 8.2 x less | 3613 | 1084 | 2.3 x less | 736
3 | 10 | 9.21e-05 | 9.54e-02 | 1034 x more | 1.42e-04 | 1.35e-05 | 9.5 x less | 4988 | 1485 | 2.4 x less | 742
4 | 1 | 5.45e-05 | 1.25e-03 | 22 x more | 4.94e-06 | 6.49e-06 | 0.3 x more | 67 | 14 | 3.8 x less | -
4 | 2 | 5.83e-05 | 7.20e-03 | 122 x more | 1.19e-05 | 7.65e-06 | 0.6 x less | 390 | 91 | 3.3 x less | 1673
4 | 3 | 6.57e-05 | 2.35e-02 | 357 x more | 3.39e-05 | 7.93e-06 | 3.3 x less | 1295 | 303 | 3.3 x less | 903
4 | 4 | 7.22e-05 | 4.96e-02 | 686 x more | 6.68e-05 | 1.02e-05 | 5.6 x less | 2753 | 653 | 3.2 x less | 874
4 | 5 | 9.85e-05 | 1.17e-01 | 1186 x more | 1.56e-04 | 1.74e-05 | 8.0 x less | 6588 | 1535 | 3.3 x less | 843
4 | 6 | 1.40e-04 | 1.98e-01 | 1416 x more | 2.66e-04 | 1.96e-05 | 13 x less | 11036 | 2582 | 3.3 x less | 802
4 | 7 | 1.77e-04 | 3.27e-01 | 1846 x more | 4.29e-04 | 2.93e-05 | 14 x less | 18271 | 4276 | 3.3 x less | 820
4 | 8 | 2.77e-04 | 5.97e-01 | 2153 x more | 8.33e-04 | 4.72e-05 | 17 x less | 33518 | 7736 | 3.3 x less | 760
4 | 9 | 3.82e-04 | 8.90e-01 | 2330 x more | 1.16e-03 | 6.35e-05 | 17 x less | 47086 | 10944 | 3.3 x less | 812
4 | 10 | 5.44e-04 | 1.30e+00 | 2388 x more | 1.80e-03 | 8.80e-05 | 20 x less | 73109 | 16873 | 3.3 x less | 758
Contact
Tell me if and how your are using this package. This encourages me to develop and test it further.
Most certainly there is stuff I missed, things I could have optimized even further or explained more clearly, etc. I would be really glad to get some feedback.
If you encounter any bugs, have suggestions etc. do not hesitate to open an Issue or add a Pull Requests on Git. Please refer to the contribution guidelines
Acknowledgements
Thanks to:
Steve for valuable feedback and writing tests.